PARP Research Group Universidad de Murcia

Projective Geometry
[Math functionality]

Functions related to Projective Geometry. More...

Functions

bool computeFundamentalMatrix (const QVector< QPointFMatching > &matchings, QVMatrix &F, const TQVSVD_Method svdMethod=DEFAULT_TQVSVD_METHOD)
 Obtains the fundamental matrix between two images using the 8-point algorithm.
double symmetricEpipolarDistance (const QVMatrix &F, const QPointFMatching &matching)
 Evaluate symmetric epipolar error for a fundamental matrix defined between two images and one image point correspondence.
QVVector symmetricEpipolarDistance (const QVMatrix &F, const QVector< QPointFMatching > &matchings)
 Evaluate symmetric epipolar errors for a fundamental matrix defined between two images and a list of image point correspondences.
bool computeProjectiveHomography (const QList< QPointFMatching > &matchings, QVMatrix &H)
 Obtains a planar homography from a list of point correspondences.
QVMatrix computeProjectiveHomography (const QList< QPointFMatching > &matchings)
 Obtains a planar homography from a list of point correspondences.
QVMatrix computeAffineHomography (const QList< QPointFMatching > &matchings)
 Obtains an affine homography from a list of point correspondences.
QVMatrix computeSimilarHomography (const QList< QPointFMatching > &matchings)
 Obtains a similar homography from a set of inter-image point matchings.
QVMatrix cvFindFundamentalMat (const QList< QPointFMatching > &matchings)
 Obtains the fundamental matrix between two images, using the 8 point algorithm.
QPointF applyHomography (const QVMatrix &homography, const QPointF &point)
 Maps a point using an homography.
QList< QPointF > applyHomography (const QVMatrix &homography, const QList< QPointF > &sourcePoints)
 Maps a set of points using an homography.
QVImage< uChar, 1 > applyHomography (const QVMatrix &homography, const QVImage< uChar, 1 > &image, const int interpolation=IPPI_INTER_CUBIC)
 Performs an homography distortion on an image.
QVImage< uChar, 3 > applyHomography (const QVMatrix &homography, const QVImage< uChar, 3 > &image, const int interpolation=IPPI_INTER_CUBIC)
 Performs an homography distortion on an image.
void getCameraPosesFromEssentialMatrix (const QVMatrix &E, QVMatrix &R1, QVMatrix &R2, QV3DPointF &t)
 Decomposes an essential matrix and obtains the corresponding pair of camera poses.
bool testCheiralityForCameraPoses (const QVMatrix &sourceRt, const QPointF &sourceProjection, const QVMatrix &destRt, const QPointF &destProjection)
 Tests if two camera poses satisfy the cheirality condition for the reconstruction of a 3D point.
QVMatrix linearCameraResection (const QList< QPointF > &points2d, const QList< QV3DPointF > &points3d)
 Obtains the camera matrix from a set of correspondences between 3D points and their respective image projections.
QV3DPointF linear3DPointTriangulation (const QVector< QVMatrix > &cameraMatrices, const QHash< int, QPointF > &projectionsOfAPoint, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of a 3D point from its projection on several views, and their corresponding camera matrices.
QV3DPointF linear3DPointTriangulation (const QList< QVMatrix > &cameraMatrices, const QList< QPointF > &projectionsOfAPoint, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of a 3D point from its projection on several views, and their corresponding camera matrices.
QV3DPointF linear3DPointTriangulation (const QPointF &point1, const QVMatrix &P1, const QPointF &point2, const QVMatrix &P2, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of a 3D point from its projection on two images, and their corresponding camera matrices.
QV3DPointF linear3DPointTriangulation (const QPointFMatching &matching, const QVMatrix &P1, const QVMatrix &P2, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of a 3D point from its projection on two images, and their corresponding camera matrices.
QV3DPointF linear3DPointTriangulation (const QPointFMatching &matching, const QVCameraPose &pose1, const QVCameraPose &pose2, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of a 3D point from its projection on two images, and their corresponding camera matrices.
QList< QV3DPointF > linear3DPointsTriangulation (const QList< QVEuclideanMapping3 > &cameras, const QList< QHash< int, QPointF > > &pointProjections, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.
QList< QV3DPointF > linear3DPointsTriangulation (const QList< QVEuclideanMapping3 > &cameras, const QVector< QHash< int, QPointF > > &pointProjections, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.
QList< QV3DPointF > linear3DPointsTriangulation (const QList< QVCameraPose > &cameras, const QList< QHash< int, QPointF > > &pointProjections, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.
QList< QV3DPointF > linear3DPointsTriangulation (const QList< QVCameraPose > &cameras, const QVector< QHash< int, QPointF > > &pointProjections, const TQVSVD_Method method=DEFAULT_TQVSVD_METHOD)
 Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.
bool getCameraFocals (const QList< QPointFMatching > &matchings, double &focal1, double &focal2, const QPointF principalPoint1=QPointF(0.0, 0.0), const QPointF principalPoint2=QPointF(0.0, 0.0), const GSLMultiminFDFMinimizerType gslMinimizerAlgorithm=VectorBFGS, const int optimizationIterations=50)
 Estimates the focal lengths for two cameras,.
double computeCameraFocalFromPlanarHomography (const QVMatrix &H, int w, int h, bool byzero=false)
 Compute camera focal from a planar homography.
QVCameraPose getCameraPoseFromCalibratedHomography (const QVMatrix &K, const QVMatrix &H)
 Estimates the camera pose form the intrinsic calibration and a planar homography.
QVEuclideanMapping3 optimizeReprojectionErrorForCameraPose (const QVEuclideanMapping3 &camera0, const QList< QPointF > &points2D, const QList< QV3DPointF > &points3D, const int iterations=5)
 Improves the estimated location of a camera pose by refining its reprojection error.
QV3DPointF optimizeReprojectionErrorFor3DPoint (const QV3DPointF &initialPoint3D, const QList< QVEuclideanMapping3 > &cameraPoses, const QHash< int, QPointF > &projectionsOfAPoint, const int iterations=5, const double lambda=1e+0)
 Improves the estimated location of a 3D point by refining its reprojection error.
QVCameraPose optimizeReprojectionErrorForCameraPoseCauchy (const QVCameraPose &cameraPose, const QList< QPointF > &points2D, const QList< QV3DPointF > &points3D, const int iterations, const double lambda=1e-5, const double sigma=3.0)
 Improves the estimated location of a camera pose by refining its reprojection error robustified by a Cauchy distribution.

Detailed Description

Functions related to Projective Geometry.

The projective geometry is the study of the geometric properties of physical objects when projected in the image plane. It provides theoretical tools to obtain 3D reconstructions and measurements of real world objects and scenes from the geometry and location of their distinctive features in images.

In this module you can find functions to:

  • Obtain the camera pose and location of 3D points of a scene, provided point correspondences between the images.
  • Estimate planar, euclidean and affine homographies from a set of image to plane point correspondences.
  • Estimate the fundamental matrix from a set of image point correspondences between two views.
  • Project points using an homography. In the case of planar homographies, project points from the image to the plane, and viceversa.
  • Triangulate 3D points provided the set of camera poses for the views where they appear and their projections on them.
  • Resect the pose of a camera, provided a set of 3D to image point correspondences.

Most of these algorithms are described in the book Multiple View Geometry in Computer Vision by R. Hartley and A. Zisserman. The references to this book in this documentation correspond to the second edition.

3D reconstruction from 2 views

From fundamental and essential matrices.

Function Documentation

bool computeFundamentalMatrix ( const QVector< QPointFMatching > &  matchings,
QVMatrix &  F,
const TQVSVD_Method  svdMethod = DEFAULT_TQVSVD_METHOD 
)

Obtains the fundamental matrix between two images using the 8-point algorithm.

This function obtains the fundamental matrix between two images using the 8-point algorithm. It is faster than the overloaded version.

Parameters:
matchings list of 8 or more point matchings.
F output fundamental matrix.
svdMethod method used in several SVD internal decompositions of the algorithm.
Returns:
True if the fundamental matrix was found, false otherwise.

Definition at line 208 of file qvepipolar.cpp.

Referenced by getCameraFocals(), and linearCameraPairInitialization().

double symmetricEpipolarDistance ( const QVMatrix &  F,
const QPointFMatching &  matching 
)

Evaluate symmetric epipolar error for a fundamental matrix defined between two images and one image point correspondence.

This function returns the epipolar error defined for the image point correspondence with the following expression:

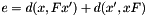
$ e = d(x, Fx') + d(x', xF) $

Where 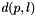$ d(p,l) $ is the euclidean distance in the 2D plane between the point 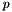$ p $ and the line $ l $.

Parameters:
F Fundamental matrix.
matching Image point matching.
Returns:
The symmetric epipolar distance $ e $.

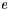Definition at line 253 of file qvepipolar.cpp.

Referenced by symmetricEpipolarDistance().

QVVector symmetricEpipolarDistance ( const QVMatrix &  F,
const QVector< QPointFMatching > &  matchings 
)

Evaluate symmetric epipolar errors for a fundamental matrix defined between two images and a list of image point correspondences.

This function returns a vector containing the symmetric epipolar errors defined for the image point correspondences with the following expression:

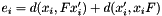
$ e_i = d(x_i, Fx'_i) + d(x'_i, x_i F) $

Where 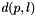$ d(p,l) $ is the euclidean distance in the 2D plane between the point 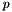$ p $ and the line $ l $.

Parameters:
F fundamental matrix.
matchings list of point matchings.
Returns:
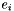A vector, containing the distance $ e_i $ for each matching.

Definition at line 302 of file qvepipolar.cpp.

bool computeProjectiveHomography ( const QList< QPointFMatching > &  matchings,
QVMatrix &  H 
)

Obtains a planar homography from a list of point correspondences.

This function obtains the homography matrix 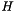$ H $ corresponding to the projective transformation which most closely map a set of four or more point correspondences.

These projective homographies can be used to obtain a frontal view of any planar figure appearing in an image. The following is an example of planar rectification:

rectification_homography.png

Image on the left is the original picture obtained with a pin-hole camera. Image on the right was obtained mapping the pixels in the original image with the planar homography obtained using the function ComputeProjectiveHomography.

The homography 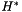$ H^* $is obtained identifying the four corners of the chessboard, and their corresponding coordinates in the plane of the chessboard:

QList< QPair<QPointF, QPointF> > matchings;
matchings.append(QPair<QPointF, QPointF>(QPointF(-171,109),     QPointF(-100,+100)));
matchings.append(QPair<QPointF, QPointF>(QPointF(-120,31),      QPointF(-100,-100)));
matchings.append(QPair<QPointF, QPointF>(QPointF(117,53),       QPointF(+100,-100)));
matchings.append(QPair<QPointF, QPointF>(QPointF(11,115),       QPointF(+100,+100)));

const QVMatrix H = ComputeProjectiveHomography(matchings);

by solving the following inequation:

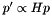
$ p' \propto H p $

maximizing the average of the algebraic reprojection error for the point matchings 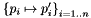$ \left\{ p_i \mapsto p_i' \right\} _{i=1..n} $ contained in the matchings list:

$ H^* = \arg\max \displaystyle\sum\limits_{i=0}^n \left[ p_i' \right] _\times H p_i $

The points in the original image can be mapped with the homography matrix 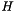$ H $ using the ApplyHomography functions.

See also:
ApplyHomography(const QVMatrix &, const QPointF &)
ApplyHomography(const QVMatrix &, const QList<QPointF> &)
Parameters:
matchings list of point matchings from the original location, to the destination location.
H output homography matrix
Returns:
false if the number of matchings is less than 4. True otherwise.

Definition at line 131 of file qvprojective.cpp.

Referenced by computeProjectiveHomography().

QVMatrix computeProjectiveHomography ( const QList< QPointFMatching > &  matchings  ) 

Obtains a planar homography from a list of point correspondences.

Deprecated:
This version of computeProjectiveHomography is deprecated. Use computeProjectiveHomography(const QList<QPointFMatching>&,QVMatrix&) instead
Parameters:
matchings list of point matchings from the original location, to the destination location.

Definition at line 1329 of file qvprojective.cpp.

QVMatrix computeAffineHomography ( const QList< QPointFMatching > &  matchings  ) 

Obtains an affine homography from a list of point correspondences.

This function obtains the homography matrix 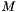$ M $ which most closely maps the source points to their destination, in the input point matching list. This homography matrix corresponds to an affine transformation.

The function returns the matrix corresponding to the planar homography, from a list of three or more point correspondences between the location of those points at the source plane and their location in the destination plane.

Usage: 

QList< QPair<QPointF, QPointF> > matchings;
matchings.append(QPair<QPointF, QPointF>(QPointF(-171,109),     QPointF(-100,+100)));
matchings.append(QPair<QPointF, QPointF>(QPointF(-120,31),      QPointF(-100,-100)));
matchings.append(QPair<QPointF, QPointF>(QPointF(117,53),       QPointF(+100,-100)));

const QVMatrix M = ComputeAffineHomography(matchings);

Any point 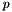$ p $ from the 2D plane can be mapped to another point in the plane 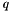$ q $ with an affine matrix 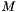$ M $ using the following C++ code:

QPointF q = M * QVVector::homogeneousCoordinates(p);

Or by using the ApplyHomography functions.

See also:
ApplyHomography(const QVMatrix &, const QPointF &)
ApplyHomography(const QVMatrix &, const QList<QPointF> &)
Parameters:
matchings list of point matchings from the original location, to the destination location.

Definition at line 227 of file qvprojective.cpp.

QVMatrix computeSimilarHomography ( const QList< QPointFMatching > &  matchings  ) 

Obtains a similar homography from a set of inter-image point matchings.

A similar transformation is obtained by composing an euclidean transformation with a scaling.

This function obtains a similar mapping between the source an destination locations of a set of point matchings. The mapping is returned as a 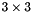$ 3 \times 3 $ matrix which can be multiplied to the source location of each mapping point in homogeneous coordinates, to obtain the location of the mapped point.

The returned matrix has the following structure:

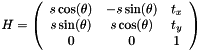
$ H = \left( \begin{array}{ccc} s \cos(\theta) & -s \sin (\theta) & t_x \\ s \sin(\theta) & s \cos (\theta) & t_y \\ 0 & 0 & 1 \end{array} \right) $

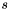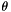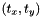Where $ s $ is the scale factor, and $ \theta $ and $ (t_x, t_y) $ are the rotation angle and translation vector of the euclidean mapping respectively.

Definition at line 275 of file qvprojective.cpp.

QVMatrix cvFindFundamentalMat ( const QList< QPointFMatching > &  matchings  ) 

Obtains the fundamental matrix between two images, using the 8 point algorithm.

This function performs point normalization to robustly obtain the F matrix.

Note:
This function is based on functionality from the OpenCV library. Thus compatibility with that library must be enabled to be available.
Parameters:
matchings list containing at least 8 image point correspondences.
Deprecated:
Use computeFundamentalMatrix to estimate the fundamental matrix using the 8 point algorithm, or call directly to the OpenCV cvFindFundamentalMat function.

Definition at line 540 of file qvprojective.cpp.

Referenced by cvFindFundamentalMat(), and getCameraFocals().

QPointF applyHomography ( const QVMatrix &  homography,
const QPointF &  point 
)

Maps a point using an homography.

This function maps a point 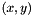$ (x, y) $ in the 2D plane, using a planar homography. The homography is represented as a 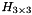$ H_{3 \times 3} $ matrix. These matrices can be obtained using methods like ComputeSimilarHomography, ComputeProjectiveHomography, or ComputeAffineHomography from a set of point correspondences between the original 2D plane, and the mapped plane.

The output of the function is a point 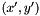$ (x', y') $ which satisfies the following equation:

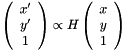
$ \left(\begin{array}{c} x' \\ y' \\ 1 \end{array}\right) \propto H \left(\begin{array}{c} x \\ y \\ 1 \end{array}\right) $

See also:
ComputeSimilarHomography
ComputeAffineHomography
ComputeProjectiveHomography
Parameters:
homography The homography transformation matrix
point Point to apply the homography transformation

Definition at line 646 of file qvprojective.cpp.

Referenced by applyHomography(), and correctIntrinsics().

QList<QPointF> applyHomography ( const QVMatrix &  homography,
const QList< QPointF > &  sourcePoints 
)

Maps a set of points using an homography.

This is an overloaded version of the ApplyHomography(const QVMatrix &, const QPointF &) function provided by convenience. This function takes a list of points from the 2D plane, and an homography matrix as inputs. The output will be a list of points obtained by mapping the points from the input list, using the homography.

See also:
ApplyHomography(const QVMatrix &, const QPointF &)
ComputeSimilarHomography
ComputeAffineHomography
ComputeProjectiveHomography
Parameters:
homography The homography transformation matrix
sourcePoints Points to apply the homography transformation

Definition at line 657 of file qvprojective.cpp.

QVImage<uChar, 1> applyHomography ( const QVMatrix &  homography,
const QVImage< uChar, 1 > &  image,
const int  interpolation = IPPI_INTER_CUBIC 
)

Performs an homography distortion on an image.

The homography is represented as a 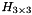$ H_{3 \times 3} $ matrix. These matrices can be obtained using methods like ComputeSimilarHomography, ComputeProjectiveHomography, or ComputeAffineHomography.

This function takes a single channel image, and an homography matrix as inputs. Each point 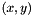$ (x, y) $ in the input image is mapped to its location in the resulting image 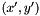$ (x', y') $ using the homography $ H $ as follows:

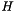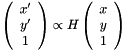
$ \left(\begin{array}{c} x' \\ y' \\ 1 \end{array}\right) \propto H \left(\begin{array}{c} x \\ y \\ 1 \end{array}\right) $

See also:
ComputeSimilarHomography
ComputeAffineHomography
ComputeProjectiveHomography
Parameters:
homography The homography transformation matrix
image The input image to distort
interpolation Type of interpolation. Possible values for this parameter are:

  • IPPI_INTER_NN. Nearest neighbor interpolation
  • IPPI_INTER_LINEAR. Linear interpolation
  • IPPI_INTER_CUBIC. Cubic interpolation
Note:
This function is based on functionality from the Intel IPP library. Thus compatibility with that library must be enabled to be available.

Definition at line 666 of file qvprojective.cpp.

QVImage<uChar, 3> applyHomography ( const QVMatrix &  homography,
const QVImage< uChar, 3 > &  image,
const int  interpolation = IPPI_INTER_CUBIC 
)

Performs an homography distortion on an image.

The homography is represented as a 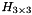$ H_{3 \times 3} $ matrix. These matrices can be obtained using methods like ComputeSimilarHomography, ComputeProjectiveHomography, or ComputeAffineHomography.

This function takes a three channel image, and an homography matrix as inputs. Each point 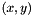$ (x, y) $ in the input image is mapped to its location in the resulting image 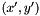$ (x', y') $ using the homography $ H $ as follows:

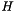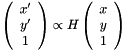
$ \left(\begin{array}{c} x' \\ y' \\ 1 \end{array}\right) \propto H \left(\begin{array}{c} x \\ y \\ 1 \end{array}\right) $

See also:
ComputeSimilarHomography
ComputeAffineHomography
ComputeProjectiveHomography
Parameters:
homography The homography transformation matrix
image The input image to distort
interpolation Type of interpolation. Possible values for this parameter are:

  • IPPI_INTER_NN. Nearest neighbor interpolation
  • IPPI_INTER_LINEAR. Linear interpolation
  • IPPI_INTER_CUBIC. Cubic interpolation
Note:
This function is based on functionality from the Intel IPP library. Thus compatibility with that library must be enabled to be available.

Definition at line 673 of file qvprojective.cpp.

void getCameraPosesFromEssentialMatrix ( const QVMatrix &  E,
QVMatrix &  R1,
QVMatrix &  R2,
QV3DPointF &  t 
)

Decomposes an essential matrix and obtains the corresponding pair of camera poses.

This function obtains the four possible pairs of valid camera poses from an essential matrix:

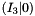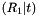
  • $ \left( I_3|0 \right) $ and $ \left( R_1|t \right) $
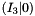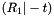
  • $ \left( I_3|0 \right) $ and $ \left( R_1|-t \right) $
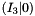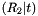
  • $ \left( I_3|0 \right) $ and $ \left( R_2|t \right) $
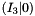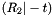
  • $ \left( I_3|0 \right) $ and $ \left( R_2|-t \right) $

These camera poses satisfy the following equation:

$ E \propto \left[ t \right] _\times R_i $

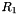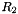This function returns the two rotation matrices ($ R_1 $ and $ R_2 $) and the vector 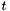$ t $ from those expressions.

See section 9.6.2 from Multiple View Geometry in Computer Vision for more info on decomposing the essential matrix to obtain the camera poses.

Note:
The function testCheiralityForCameraPoses can be used to test which one of these configurations corresponds to a valid 3D reconstruction.
Parameters:
E The input essential matrix.
R1 Output param containing the first possible rotation matrix.
R2 Output param containing the second possible rotation matrix.
t Output param containing the translation vector.

Definition at line 1219 of file qvprojective.cpp.

Referenced by linearCameraPairInitialization().

bool testCheiralityForCameraPoses ( const QVMatrix &  sourceRt,
const QPointF &  sourceProjection,
const QVMatrix &  destRt,
const QPointF &  destProjection 
)

Tests if two camera poses satisfy the cheirality condition for the reconstruction of a 3D point.

This function reconstructs a 3D point from its projections on two image views, and test whether the triangulated location is in front or behind of the cameras. If the point is not in front of both cameras, the 3D reconstruction obtained from these camera poses will be incorrect.

See chapter 20 from Multiple View Geometry in Computer Vision for more info on cheirality.

Parameters:
sourceRt Camera pose for the first view.
sourceProjection Projection of the point used to test cheirality on the first view.
destRt Camera pose for the second view.
destProjection Projection of the point used to test cheirality on the second view.
Returns:
True if the point reconstruction is in front of both camera poses, false otherwise.
See also:
getCameraPosesFromEssentialMatrix

Definition at line 1241 of file qvprojective.cpp.

Referenced by linearCameraPairInitialization(), and testCheirality().

QVMatrix linearCameraResection ( const QList< QPointF > &  points2d,
const QList< QV3DPointF > &  points3d 
)

Obtains the camera matrix from a set of correspondences between 3D points and their respective image projections.

The following formula models the relation between a set of points from the 3D world 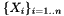$ \{ X_i \}_{i=1..n} $ and their projections 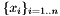$ \{ x_i \}_{i=1..n} $ on an image:

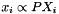
$ x_i \propto P X_i $

This function uses a direct linear transformation (DLT) to obtain the camera matrix 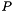$ P $ from a given set of 3D points and their corresponding image points.

For more information about the linear camera resection, check chapter 7 of 'Multiple View Geometry in Computer Vision', section 7.1.

Parameters:
points2d List containing the points from the image.
points3d List containing the 3D points.
Returns:
The camera matrix $ P $.

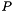Definition at line 896 of file qvprojective.cpp.

QV3DPointF linear3DPointTriangulation ( const QVector< QVMatrix > &  cameraMatrices,
const QHash< int, QPointF > &  projectionsOfAPoint,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of a 3D point from its projection on several views, and their corresponding camera matrices.

This is an overloaded version of the function linear3DPointTriangulation(const QList<QVMatrix> &, const QList<QPointF> &), provided for convenience.

This version does not require that the point were visible from every camera in the input camera list. The point projections are provided in a QHash structure. Each key in that structure is the index at the camera list of the camera corresponding to the point projection.

See also:
linear3DPointTriangulation(const QList<QVMatrix> &, const QList<QPointF> &);

Definition at line 1011 of file qvprojective.cpp.

QV3DPointF linear3DPointTriangulation ( const QList< QVMatrix > &  cameraMatrices,
const QList< QPointF > &  projectionsOfAPoint,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of a 3D point from its projection on several views, and their corresponding camera matrices.

Using the projection formula:

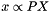
$ x \propto P X $

This function triangulates the location of the 3D point 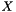$ X $, provided the projections 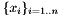$ \{x_i\}_{i=1..n}$ on several views, and the camera matrices 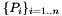$ \{P_i\}_{i=1..n}$ for those views.

The method used is described at section 12.2 from Multiple View Geometry in Computer Vision.

Parameters:
cameraMatrices list of camera matrices for the different views.
projectionsOfAPoint list of projections of the 3D point for the different views.
Returns:
The triangulated location for the point.

Definition at line 969 of file qvprojective.cpp.

Referenced by linear3DPointsTriangulation(), linear3DPointTriangulation(), and testCheiralityForCameraPoses().

QV3DPointF linear3DPointTriangulation ( const QPointF &  point1,
const QVMatrix &  P1,
const QPointF &  point2,
const QVMatrix &  P2,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of a 3D point from its projection on two images, and their corresponding camera matrices.

Using the projection formula:

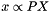
$ x \propto P X $

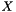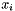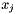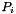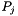This function triangulates the location of the 3D point $ X $, provided the projections $ x_i$ and $ x_j$ on two views, and the camera matrices $ P_i$ and $ P_j$ for those views.

The method used is described at section 12.2 from Multiple View Geometry in Computer Vision.

Parameters:
point1 The projected location of the 3D point in the first image.
P1 The camera matrix for the first image.
point2 The projected location of the 3D point in the second image.
P2 The camera matrix for the second image.
Returns:
The triangulated location for the point.
Deprecated:
use linear3DPointTriangulation(const QPointFMatching &, const QVMatrix &, const QVMatrix &, const TQVSVD_Method) instead.

Definition at line 1337 of file qvprojective.cpp.

QV3DPointF linear3DPointTriangulation ( const QPointFMatching &  matching,
const QVMatrix &  P1,
const QVMatrix &  P2,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of a 3D point from its projection on two images, and their corresponding camera matrices.

Using the projection formula:

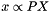
$ x \propto P X $

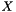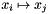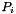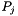This function triangulates the location of the 3D point $ X $, provided the point matchings $ x_i \mapsto x_j $ between two views, and the camera matrices $ P_i$ and $ P_j$ for those views.

The method used is described at section 12.2 from Multiple View Geometry in Computer Vision.

Parameters:
matching Point matching containing the projections of each 3D point at both cameras.
P1 The camera matrix for the first image.
P2 The camera matrix for the second image.
method The method to solve the linear system.
Returns:
The triangulated location for the point.

Definition at line 1050 of file qvprojective.cpp.

QV3DPointF linear3DPointTriangulation ( const QPointFMatching &  matching,
const QVCameraPose &  pose1,
const QVCameraPose &  pose2,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of a 3D point from its projection on two images, and their corresponding camera matrices.

Using the projection formula:

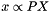
$ x \propto P X $

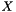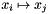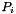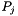This function triangulates the location of the 3D point $ X $, provided the point matchings $ x_i \mapsto x_j $ between two views, and the camera matrices $ P_i$ and $ P_j$ for those views.

The method used is described at section 12.2 from Multiple View Geometry in Computer Vision.

Parameters:
matching Point matching containing the projections of each 3D point at both cameras.
pose1 The camera pose for the first image.
pose2 The camera pose for the second image.
method The method to solve the linear system.
Returns:
The triangulated location for the point.

Definition at line 1088 of file qvprojective.cpp.

QList<QV3DPointF> linear3DPointsTriangulation ( const QList< QVEuclideanMapping3 > &  cameras,
const QList< QHash< int, QPointF > > &  pointProjections,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.

Using function linear3DPointTriangulation, the locations of several 3D points are triangulated with this function.

Parameters:
cameras List of cameras.
pointProjections Container for the point projections. Each element in this list corresponds to a 3D point. These elements are hash tables, containing the point image projections, indexed by the number of the camera.
Returns:
The triangulated locations for the points.

Definition at line 1111 of file qvprojective.cpp.

Referenced by reconstructionError().

QList<QV3DPointF> linear3DPointsTriangulation ( const QList< QVEuclideanMapping3 > &  cameras,
const QVector< QHash< int, QPointF > > &  pointProjections,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.

This is an overloaded version of the previous function.

Parameters:
cameras List of cameras.
pointProjections Container for the point projections. Each element in this list corresponds to a 3D point. These elements are hash tables, containing the point image projections, indexed by the number of the camera.
Returns:
The triangulated locations for the points.

Definition at line 1127 of file qvprojective.cpp.

QList<QV3DPointF> linear3DPointsTriangulation ( const QList< QVCameraPose > &  cameras,
const QList< QHash< int, QPointF > > &  pointProjections,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.

Using function linear3DPointTriangulation, the locations of several 3D points are triangulated with this function.

Parameters:
cameras List of cameras.
pointProjections Container for the point projections. Each element in this list corresponds to a 3D point. These elements are hash tables, containing the point image projections, indexed by the number of the camera.
Returns:
The triangulated locations for the points.

Definition at line 1143 of file qvprojective.cpp.

QList<QV3DPointF> linear3DPointsTriangulation ( const QList< QVCameraPose > &  cameras,
const QVector< QHash< int, QPointF > > &  pointProjections,
const TQVSVD_Method  method = DEFAULT_TQVSVD_METHOD 
)

Recovers the location of several 3D points from their projections on different views, and the corresponding camera matrices.

This is an overloaded version of the previous function.

Parameters:
cameras List of cameras.
pointProjections Container for the point projections. Each element in this list corresponds to a 3D point. These elements are hash tables, containing the point image projections, indexed by the number of the camera.
Returns:
The triangulated locations for the points.

Definition at line 1159 of file qvprojective.cpp.

bool getCameraFocals ( const QList< QPointFMatching > &  matchings,
double &  focal1,
double &  focal2,
const QPointF  principalPoint1 = QPointF(0.0, 0.0),
const QPointF  principalPoint2 = QPointF(0.0, 0.0),
const GSLMultiminFDFMinimizerType  gslMinimizerAlgorithm = VectorBFGS,
const int  optimizationIterations = 50 
)

Estimates the focal lengths for two cameras,.

This function can be used to calibrate two cameras, provided a rough approximation of their principal point locations, and a list of point correspondences between two images.

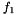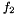It first obtains two initial estimations for the focal lengths $ f_1 $ and $ f_2 $ of the cameras using the procedure described in [1]. These focal distances are refined by optimizing the following calibration error function:

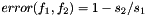
$ error(f_1, f_2) = 1 - s_2 / s_1 $

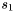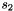where the values $ s_1 $ and $ s_2 $ correspond to the first and second singular values of the following matrix:

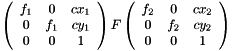
$ \left(\begin{array}{ccc} f_1 & 0 & cx_1 \\ 0 & f_1 & cy_1 \\ 0 & 0 & 1 \\ \end{array}\right) F \left(\begin{array}{ccc} f_2 & 0 & cx_2 \\ 0 & f_2 & cy_2 \\ 0 & 0 & 1 \\ \end{array}\right) $

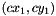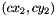where $ (cx_1, cy_1) $ and $ (cx_2, cy_2) $ are the provided rough approximations for the principal points of the first and second camera respectively, and 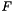$ F $ is the fundamental matrix obtained from the list of point correspondences.

[1] Estimation of Relative Camera Positions for Uncalibrated Cameras. R. Hartley. Proceedings of the Second European Conference on Computer Vision, 1992.

Parameters:
matchings List of point matchings between the two images.
focal1 This variable will contain the focal for the first camera in return.
focal2 This variable will contain the focal for the second camera in return.
principalPoint1 Rough approximation for the principal point of the first camera.
principalPoint2 Rough approximation for the principal point of the second camera.
gslMinimizerAlgorithm Algorithm to use in the optimization step of the focal calibration.
optimizationIterations Number of iterations to perform at the optimization step.
Note:
This function requires GSL compatibility.
Returns:
false if a numerical error was found, and the focal lengths could not be estimated, true otherwise.

Definition at line 512 of file getCameraFocals.cpp.

double computeCameraFocalFromPlanarHomography ( const QVMatrix &  H,
int  w,
int  h,
bool  byzero = false 
)

Compute camera focal from a planar homography.

This function computes the camera focal by solving for diagonal matrix IAC 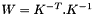$ W=K^{-T}.K^{-1} $, taking into account that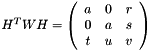 $ H^T W H = \left( \begin{array}{ccc} a & 0 & r \\ 0 & a & s \\ t & u & v \end{array} \right) $

This is equivalent to two different constraints in the entries of H, one of them to force

(1) $ (H^T W H)(0,0) = (H^T W H)(1,1) $

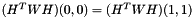
and the other to force

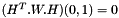
(2) $ (H^T.W.H)(0,1)=0 $

If we want to use the first condition, we set byzero to false; if we want to use de second, we set byzero to true. (Of course, we could have also used both conditions at the same time, and solve by minimum squares).

Parameters:
H planar homography matrix
w horizontal coordinate for the principal point of the image
h vertical coordinate for the principal point of the image
byzero If true, use equation (1) to solve for the focal value. Otherwise, use equation (2)

Definition at line 1283 of file qvprojective.cpp.

QVCameraPose getCameraPoseFromCalibratedHomography ( const QVMatrix &  K,
const QVMatrix &  H 
)

Estimates the camera pose form the intrinsic calibration and a planar homography.

Parameters:
K Intrinsic calibration matrix for the camera.
H Planar homography.

Definition at line 1292 of file qvprojective.cpp.

QVEuclideanMapping3 optimizeReprojectionErrorForCameraPose ( const QVEuclideanMapping3 &  camera0,
const QList< QPointF > &  points2D,
const QList< QV3DPointF > &  points3D,
const int  iterations = 5 
)

Improves the estimated location of a camera pose by refining its reprojection error.

Provided a set of 3D points and their estimated projections on an image, this function improves the pose for that view, by refining the 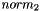$ norm_2 $ of the reprojection error using the Levenberg-Marquardt optimization.

Parameters:
cameraPose Initial camera pose.
points2D List of image projections for the points
points3D List of 3D coordinates for the points
iterations Number of Levenberg-Marquard iterations to perform
Returns:
An improved camera pose.

Definition at line 154 of file qvreprojectionerror.cpp.

QV3DPointF optimizeReprojectionErrorFor3DPoint ( const QV3DPointF &  initialPoint3D,
const QList< QVEuclideanMapping3 > &  cameraPoses,
const QHash< int, QPointF > &  projectionsOfAPoint,
const int  iterations = 5,
const double  lambda = 1e+0 
)

Improves the estimated location of a 3D point by refining its reprojection error.

Provided the estimated projections of a 3D point on a set of views, and the estimated camera poses for those views, this function improves the estimated location of the 3D point by refining the 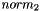$ norm_2 $ of the reprojection error using the Levenberg-Marquardt optimization.

Parameters:
initialPoint3D Initial 3D point location.
cameraPoses List of the views camera poses.
projectionsOfAPoint List of projections of the 3D point on the views.
iterations Number of iterations to refine reprojection error.
lambda Value to increase the diagonal of the Hessian matrix in the Levenberg-Marquardt algorithm.
Returns:
An improved location for the 3D point.

Definition at line 267 of file qvreprojectionerror.cpp.

QVCameraPose optimizeReprojectionErrorForCameraPoseCauchy ( const QVCameraPose &  cameraPose,
const QList< QPointF > &  points2D,
const QList< QV3DPointF > &  points3D,
const int  iterations,
const double  lambda = 1e-5,
const double  sigma = 3.0 
)

Improves the estimated location of a camera pose by refining its reprojection error robustified by a Cauchy distribution.

This function optimizes the pose of a view using the Levenberg-Marquardt optimization, provided the image projections of a set of 3D points.

This method assumes a Cauchy distribution for the reprojection residuals, to reduce the impact of outliers in the cost error, and improve the obtained camera pose.

Parameters:
cameraPose Initial camera pose.
points2D List of image projections for the points
points3D List of 3D coordinates for the points
iterations Number of Levenberg-Marquard iterations to perform
lambda Increment of the diagonal elements for the estimated Hessian matrix
sigma standard deviation to the cost function (negative log-likelihood)
Returns:
An improved camera pose.

Definition at line 455 of file qvreprojectionerror.cpp.



QVision framework. PARP research group. Copyright © 2007, 2008, 2009, 2010, 2011.