PARP Research Group Universidad de Murcia

Numerical analisis and function minimization
[Math functionality]

Function optimization and numerical derivative evaluation. More...

Classes

class  QVFunction< Input, Output >
 Base class for function objects. More...
class  QVJacobian
 Class to create jacobian functions. More...

Enumerations

enum  GSLMinFMinimizer { GoldenSection = 0, BrentMinimization = 1 }
 

GSL Minimization algorithms.

More...
enum  GSLMultiminFDFMinimizerType { ConjugateFR = 0, ConjugatePR = 1, VectorBFGS = 2, SteepestDescent = 3 }
 

GSL multidimensional minimization algorithms using gradient information.

More...
enum  GSLMultiminFDFSolverType { LMScaledDerivative = 0, LMDerivative = 1 }
 

GSL multidimensional solving.

More...

Functions

const QVVector qvEstimateGradient (QVFunction< QVVector, double > &function, const QVVector &point, const double h=1e-6)
 Estimates the gradient vector for the function using the forward two-points rule for the derivative approximation.
const QVMatrix qvEstimateJacobian (QVFunction< QVVector, QVVector > &function, const QVVector &point, const double h=1e-6)
 Estimates the Jacobian matrix for the function using the forward two-points rule for the derivative approximation.
const QVMatrix qvEstimateHessian (QVFunction< QVVector, double > &function, const QVVector &point, const double h=1e-3)
 Estimates the hessian matrix for the function using the forward two-point rule for the derivative approximation.
bool qvGSLMinimizeFDF (const QVFunction< QVVector, double > &function, QVVector &point, const GSLMultiminFDFMinimizerType gslMinimizerAlgorithm=ConjugateFR, const int maxIterations=100, const double maxGradientNorm=1e-3, const double step=0.01, const double tol=1e-4)
 Wrapper to GSL multivariate function minimization using gradient information.
bool qvGSLMinimizeFDF (const QVFunction< QVVector, double > &function, const QVFunction< QVVector, QVVector > &gradientFunction, QVVector &point, const GSLMultiminFDFMinimizerType gslMinimizerAlgorithm=ConjugateFR, const int maxIterations=100, const double maxGradientNorm=1e-3, const double step=0.01, const double tol=1e-4)
 Wrapper to GSL multivariate function minimization using gradient information.
bool qvGSLSolveFDF (const QVFunction< QVVector, QVVector > &function, const QVFunction< QVVector, QVMatrix > &functionJacobian, QVVector &x, const GSLMultiminFDFSolverType gslSolverAlgorithm=LMScaledDerivative, const int maxIterations=100, const double maxAbsErr=1e-4, const double maxRelErr=1e-4)
 Solves a non-linear system of equations.
bool qvGSLMinimize (const QVFunction< double, double > &function, double &x, double &lower, double &upper, const GSLMinFMinimizer gslMinimizerAlgorithm=BrentMinimization, const int maxIterations=100, const double absoluteError=1e-3, const double relativeError=0.0)
 Wrapper to GSL function minimization.

Detailed Description

Function optimization and numerical derivative evaluation.

Enumeration Type Documentation

enum GSLMinFMinimizer

GSL Minimization algorithms.

See also:
qvGSLMinimize
Enumerator:
GoldenSection 

The golden section algorithm. The simplest method of bracketing the minimum of a function.

BrentMinimization 

The Brent minimization algorithm. Combines a parabolic interpolation with the golden section algorithm.

Definition at line 93 of file qvnumericalanalysis.h.

enum GSLMultiminFDFMinimizerType

GSL multidimensional minimization algorithms using gradient information.

See also:
qvGSLMinimizeFDF
Enumerator:
ConjugateFR 

Fletcher-Reeves conjugate gradient algorithm.

ConjugatePR 

Polak-Ribiere conjugate gradient algorithm.

VectorBFGS 

Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm.

SteepestDescent 

The steepest descent algorithm.

Definition at line 108 of file qvnumericalanalysis.h.

enum GSLMultiminFDFSolverType

GSL multidimensional solving.

See also:
qvGSLSolveFDF
Enumerator:
LMScaledDerivative 

Scaled Levenberg-Marquardt algorithm.

LMDerivative 

Non-scaled (faster) Levenberg-Marquardt algorithm.

Definition at line 127 of file qvnumericalanalysis.h.

Function Documentation

const QVVector qvEstimateGradient ( QVFunction< QVVector, double > &  function,
const QVVector &  point,
const double  h = 1e-6 
)

Estimates the gradient vector for the function using the forward two-points rule for the derivative approximation.

This function obtains a numerical approximation of the gradient at a given point for a function. The forward derivative formula is used to estimate each partial derivative value, component of the gradient vector:

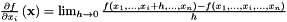
$ \frac{ \partial f}{ \partial x_i} \left( \textbf{x} \right) = \lim_{h\to 0}{f(x_1, \ldots, x_i + h, \ldots, x_n)-f(x_1, \ldots, x_i, \ldots, x_n)\over h}$

The function to estimate the gradient is provided as a QVFunction object.

Parameters:
function object containing the function to estimate gradient.
point Point to evaluate the gradient vector.
h Increment coeficient for the derivative formula.

Definition at line 28 of file qvnumericalanalysis.cpp.

Referenced by qvEstimateHessian().

const QVMatrix qvEstimateJacobian ( QVFunction< QVVector, QVVector > &  function,
const QVVector &  point,
const double  h = 1e-6 
)

Estimates the Jacobian matrix for the function using the forward two-points rule for the derivative approximation.

This function obtains a numerical approximation of the Jacobian of a 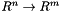$ R^n \to R^m $ function at a given point. The forward derivative formula is used to estimate each partial derivative value, component of the Jacobian:

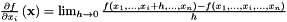
$ \frac{ \partial f}{ \partial x_i} \left( \textbf{x} \right) = \lim_{h\to 0}{f(x_1, \ldots, x_i + h, \ldots, x_n)-f(x_1, \ldots, x_i, \ldots, x_n)\over h}$

The function to estimate the gradient is provided as a QVFunction object.

Parameters:
function function object to estimate Jacobian.
point Point to evaluate the Jacobian matrix.
h Increment coeficient for the derivative formula.

Definition at line 42 of file qvnumericalanalysis.cpp.

const QVMatrix qvEstimateHessian ( QVFunction< QVVector, double > &  function,
const QVVector &  point,
const double  h = 1e-3 
)

Estimates the hessian matrix for the function using the forward two-point rule for the derivative approximation.

This function obtains a numerical approximation of the hessian matrix at a given pointfor a function. The following formula is used to compute the components fo the hessian matrix:

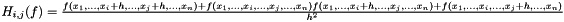
$ H_{i, j}(f) = \frac{ f(x_1, \ldots, x_i + h, \ldots, x_j + h, \ldots, x_n) + f(x_1, \ldots, x_i, \ldots, x_j, \ldots, x_n) f(x_1, \ldots, x_i + h, \ldots, x_j, \ldots, x_n) + f(x_1, \ldots, x_i, \ldots, x_j + h, \ldots, x_n) }{h^2}$

It is derived from the forward derivative formula used to estimate each partial derivative value:

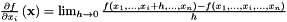
$ \frac{ \partial f}{ \partial x_i} \left( \textbf{x} \right) = \lim_{h\to 0}{f(x_1, \ldots, x_i + h, \ldots, x_n)-f(x_1, \ldots, x_i, \ldots, x_n)\over h}$

The function to estimate the hessian is provided as a QVFunction object.

Parameters:
function object containing the function to estimate hessian.
point Point to evaluate the hessian matrix.
h Increment coeficient for the derivative formula.

Definition at line 58 of file qvnumericalanalysis.cpp.

bool qvGSLMinimizeFDF ( const QVFunction< QVVector, double > &  function,
QVVector &  point,
const GSLMultiminFDFMinimizerType  gslMinimizerAlgorithm = ConjugateFR,
const int  maxIterations = 100,
const double  maxGradientNorm = 1e-3,
const double  step = 0.01,
const double  tol = 1e-4 
)

Wrapper to GSL multivariate function minimization using gradient information.

This function minimizes a multivariate function contained in a QVFunction object, using the GSL functionality for that purpose. The gradient of that function is estimated using the qvEstimateGradient function, and is used in the minimization process.

An usage example follows: 

#include <qvnumericalanalysis.h>

// Creation of a quadratic function class type
class QuadraticFunction: public QVFunction<QVVector, double>
    {
    private:
        const QVMatrix A;
        const QVVector b;
        const double c;

        double evaluate(const QVVector &x)
            {
            return x*A*x + b*x + c;
            }

    public:
        QuadraticFunction(const QVMatrix &A, const QVVector &b, const double c): QVFunction<QVVector, double>(),
            A(A), b(b), c(c)
            { }
    };

// Main code
int main()
    {
    // Example quadratic function object creation
    QVMatrix A = QVMatrix::zeros(3,3);
    QVVector b = QVVector(3,0);
    double c;

    A(0,0) = 70;        A(1,1) = 11;    A(2,2) = 130;
    b = QVVector(3); b[0] = -100; b[1] = 20; b[2] = -30;
    c = 100;

    QuadraticFunction f(A, b, c);

    // Function minimization
    QVVector minimum(3,0);
    qvGSLMinimizeFDF(f, minimum);

    std::cout << "Function minimum value = " << f(minimum) << std::endl;
    std::cout << "Reached at point = " << minimum << std::endl;;
    }
Parameters:
function Object containing the function to minimize.
point Starting point for the minimization. This vector will contain the obtained minimum when the function returns.
gslMinimizerAlgorithm Minimization algorithm. See enumeration GSLMultiminFDFMinimizerType for possible values.
maxIterations Maximum number of steps to perform by the minimization.
maxGradientNorm Minimal value of the gradient size (norm 2) to stop the minimization when reached.
step Corresponds to parameter step for the gsl_multimin_fdfminimizer_set function.
tol Corresponds to parameter tol for the gsl_multimin_fdfminimizer_set function.
Warning:
The GSL compatibility must be enabled to use this function.
Returns:
True if the search was successful. False else.
See also:
GSLMultiminFDFMinimizerType

Definition at line 100 of file qvnumericalanalysis.cpp.

Referenced by getCameraFocals().

bool qvGSLMinimizeFDF ( const QVFunction< QVVector, double > &  function,
const QVFunction< QVVector, QVVector > &  gradientFunction,
QVVector &  point,
const GSLMultiminFDFMinimizerType  gslMinimizerAlgorithm = ConjugateFR,
const int  maxIterations = 100,
const double  maxGradientNorm = 1e-3,
const double  step = 0.01,
const double  tol = 1e-4 
)

Wrapper to GSL multivariate function minimization using gradient information.

This is an overloaded version of the function qvGSLMinimizeFDF(QVFunction<QVVector, double> &, QVVector &, const GSLMultiminFDFMinimizerType, const int, const double, const double, const double) provided for convenience.

The real gradient of the function is used in the form of a vector function object, instead of the numerical approximation qvEstimateGradient to the gradient, which is less accurate and generally less efficient. An example code usage follows:

#include <qvnumericalanalysis.h>

// Creation of a quadratic function class type
class QuadraticFunction: public QVFunction<QVVector, double>
    {
    private:
        const QVMatrix A;
        const QVVector b;
        const double c;

        double evaluate(const QVVector &x)
            {
            return x*A*x + b*x + c;
            }

    public:
        QuadraticFunction(const QVMatrix &A, const QVVector &b, const double c): QVFunction<QVVector, double>(),
            A(A), b(b), c(c)
            { }
    };

// Creation of a quadratic vector function class type, corresponding to the gradient of the previous function
class QuadraticFunctionGradient: public QVFunction<QVVector, QVVector>
    {
    private:
        const QVMatrix A;
        const QVVector b;
        const double c;

        QVVector evaluate(const QVVector &x)
            {
            return A*x*2 + b;
            }

    public:
        QuadraticFunctionGradient(const QVMatrix &A, const QVVector &b, const double c): QVFunction<QVVector, QVVector>(),
            A(A), b(b), c(c)
            { }
    };

// Main code
int main()
    {
    // Example quadratic function and corresponding gradient objects creation
    QVMatrix A = QVMatrix::zeros(3,3);
    QVVector b = QVVector(3,0);
    double c;

    A(0,0) = 70;        A(1,1) = 11;    A(2,2) = 130;
    b = QVVector(3); b[0] = -100; b[1] = 20; b[2] = -30;
    c = 100;

    QuadraticFunction           f(A, b, c);
    QuadraticFunctionGradient   g(A, b, c);

    // Function minimization
    QVVector minimum(3,0);
    qvGSLMinimizeFDF(f, g, minimum);

    std::cout << "Function minimum value = " << f(minimum) << std::endl;
    std::cout << "Reached at point = " << minimum << std::endl;
    }
Parameters:
function Object containing the function to minimize.
gradientFunction Object containing the gradient vector function.
point Starting point for the minimization. This vector will contain the obtained minimum when the function returns.
gslMinimizerAlgorithm Minimization algorithm. See enumeration GSLMultiminFDFMinimizerType for possible values.
maxIterations Maximum number of steps to perform the minimization.
maxGradientNorm Minimal value of the gradient size (norm 2) to stop the minimization when reached.
step Corresponds to parameter step for the gsl_multimin_fdfminimizer_set function.
tol Corresponds to parameter tol for the gsl_multimin_fdfminimizer_set function.
Warning:
The GSL compatibility must be enabled to use this function.
Returns:
True if the search was successful. False else.
See also:
qvGSLMinimizeFDF(QVFunction<QVVector, double> &, QVVector &, const GSLMultiminFDFMinimizerType, const int, const double, const double, const double)
GSLMultiminFDFMinimizerType

Definition at line 167 of file qvnumericalanalysis.cpp.

bool qvGSLSolveFDF ( const QVFunction< QVVector, QVVector > &  function,
const QVFunction< QVVector, QVMatrix > &  functionJacobian,
QVVector &  x,
const GSLMultiminFDFSolverType  gslSolverAlgorithm = LMScaledDerivative,
const int  maxIterations = 100,
const double  maxAbsErr = 1e-4,
const double  maxRelErr = 1e-4 
)

Solves a non-linear system of equations.

This function uses a nonlinear least-squares optimization procedure to obtain a solution for a system of equations. The input of this functions is a function object, containing a 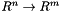$ R^n \to R^m $ function, that maps the input variables for the system, to the vector of residual values of the system of equations.

The function uses the Levenberg-Marquardt optimization algoritm to find an aproximation to a valid solution, starting from an initial guess of the solution.

The optimization finishes when performing a fixed number of maximum iterations. Also, a stopping criteria is applied. The convergence is tested by comparing the last step dx with the absolute error maxAbsErr and relative error maxRelErr to the current position x. The test is true if the following condition is achieved:

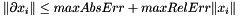
$ \|\partial x_i\| \leq maxAbsErr + maxRelErr \| x_i \| $

In that case the function stops and returns the point where the function returns the minimum value.

The following code is an usage example of this function. It fits an exponential model on some input measurements:

#include <qvnumericalanalysis.h>
class FittingErrorFunction: public QVFunction<QVVector, QVVector>
        {
        private:
        const QVVector x, y;

                QVVector evaluate(const QVVector &v)
                        {
            // Evaluate the function
            QVVector result(y.size(), 0.0);
            for (int i = 0; i < y.size(); i++)
                result[i] = v[0] * exp (-v[1] * double(x[i])) + v[2];

            // Return residuals
            return result - y;
            }

        public:
            FittingErrorFunction(const QVVector &x, const QVVector &y): QVFunction<QVVector, QVVector>(), x(x), y(y) { }
            };

class FittingErrorFunctionJacobian: public QVFunction<QVVector, QVMatrix>
        {
        private:
        const QVVector x, y;

                QVMatrix evaluate(const QVVector &v)
                        {
            FittingErrorFunction error(x, y);
            return qvEstimateJacobian(error, v);
            }

        public:
            FittingErrorFunctionJacobian(const QVVector &x, const QVVector &y): QVFunction<QVVector, QVMatrix>(), x(x), y(y) { }
            };

int main()
    {
    QVVector x, y;
    for (int i = 0; i < 40; i++)
        {
        x << double(i);
        y << 1.0 + 5 * exp (-0.1 * double(i));
        }

    // Create initial guess, and objective functions.
    QVVector v(3, 0.0);
    FittingErrorFunction function(x, y);
    FittingErrorFunctionJacobian functionJacobian(x, y);

    qvGSLSolveFDF (function, functionJacobian, v, LMScaledDerivative, 500);

    std::cout << "Solution for the system obtained at " << v << std::endl;
    }
Warning:
The GSL compatibility must be enabled to use this function.
Parameters:
function Function representing the residuals of the system of equations.
functionJacobian Jacobian of the residual function.
x Initial guess of the solution. Also, the minimum value will be stored in this variable.
gslSolverAlgorithm The algorithm to perform minimization.
maxIterations Maximum number of iterations to perform optimization.
maxAbsErr Maximal absolute error in the optimization stop condition.
maxRelErr Maximal relative error in the optimization stop condition.
bool qvGSLMinimize ( const QVFunction< double, double > &  function,
double &  x,
double &  lower,
double &  upper,
const GSLMinFMinimizer  gslMinimizerAlgorithm = BrentMinimization,
const int  maxIterations = 100,
const double  absoluteError = 1e-3,
const double  relativeError = 0.0 
)

Wrapper to GSL function minimization.

This function uses the GSL to obtain the minimum of a function, provided in a QVFunction object. An example code usage follows:

#include <qvnumericalanalysis.h>

// Creation of a sinoidal function class type
class SinoidalFunction: public QVFunction<double, double>
    {
    private:
        double evaluate(const double &x) const
            {
            return cos(x) + 1.0;
            }

    public:
        SinoidalFunction(): QVFunction<double, double>() { };
    };

int main(int argc, char *argv[])
    {
    const SinoidalFunction function;
    double x = 2.0, lower = 0.0, upper = 6.0;

    qvGSLMinimize(function, x, lower, upper);

    printf ("Minimum found at %.7f\n", x);

    exit(0);
    }
Parameters:
function Object containing the function to minimize.
x Starting value for the minimization. This variable will contain the obtained minimum when the function returns.
gslMinimizerAlgorithm Minimization algorithm. See enumeration GSLMinFMinimizer for possible values.
lower Minimal value for the search range.
upper Maximum value for the search range.
maxIterations Maximum number of steps to perform the minimization.
maxGradientNorm Minimal value of the gradient size (norm 2) to stop the minimization when reached.
absoluteError Corresponds to parameter epsabs for the gsl_min_test_interval function.
relativeError Corresponds to parameter epsrel for the gsl_min_test_interval function.
Warning:
The GSL compatibility must be enabled to use this function.
Returns:
True if the search was successful. False else.
See also:
qvGSLMinimizeFDF
GSLMinFMinimizer

Definition at line 302 of file qvnumericalanalysis.cpp.



QVision framework. PARP research group. Copyright © 2007, 2008, 2009, 2010, 2011.