PARP Research Group Universidad de Murcia

QVSparseBlockMatrix Class Reference
[Math functionality]

Implementation of sparse block matrices. More...

#include <QVSparseBlockMatrix>

List of all members.

Public Member Functions

 QVSparseBlockMatrix ()
 Default constructor for the QVSparseBlockMatrix class.
 QVSparseBlockMatrix (const int majorRows, const int majorCols, const int minorRows, const int minorCols)
 Create a sparse block matrix of a given size.
 QVSparseBlockMatrix (const int majorRows, const int majorCols, const QVMatrix &other)
 Create a sparse block matrix from a dense matrix.
int getMajorRows () const
 Get majorRows from a sparse block matrix.
int getMajorCols () const
 Get majorCols from a sparse block matrix.
int getMinorRows () const
 Get minorRows from a sparse block matrix.
int getMinorCols () const
 Get minorCols from a sparse block matrix.
 operator QVMatrix () const
 Convert a sparse block matrix into an ordinary matrix.
void setBlock (const int majorRow, const int majorCol, const QVMatrix &M)
 Set a data block.
QVMatrix & getBlock (const int majorRow, const int majorCol)
 Gets a data block.
bool isNullBlock (const int majorRow, const int majorCol) const
 Evaluate if a block contains zero values.
QList< int > getBlockRowIndexes (const int majorRow) const
 List of non-zero blocks in a block-row.
QVSparseBlockMatrix operator* (const QVSparseBlockMatrix &other) const
 Product operator for sparse block matrices.
QVVector operator* (const QVVector &vector) const
 Sparse block matrix-vector product.
QVSparseBlockMatrix dotProduct (const QVSparseBlockMatrix &other, const bool transposeFirstOperand=false, const bool transposeSecondOperand=false) const
 Dot product for sparse block matrices.
QVVector dotProduct (const QVVector &vector, const bool transposeMatrix=false) const
 Dot product for sparse block matrices with vectors.
QVSparseBlockMatrix & operator= (const QVSparseBlockMatrix &other)
 Copy operator.
void clear ()
 Set matrix to zero.

Static Public Member Functions

static QVSparseBlockMatrix randomSquare (const int NB, const int N, const double NZProb, const bool symmetric=true, const bool positive=true)
 Generates a random square sparse block matrix The sparse block matrix must have compatible block sizes, and major sizes, with the vecto size.

Detailed Description

Implementation of sparse block matrices.

Each sparse block matrix is implemented as a bidimensional array of QVMatrix objects. The sparse matrices have two kind of indexes: major indexes, that access the bidimensional array, and minor indexes, that access elements in the matrix objects inside the cells of the array.

The following is an example sparse matrix of size 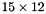$ 15 \times 12 $. It contains 12 blocks (or submatrices) of size 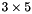$ 3 \times 5 $ (minor dimensions), arranged in an array of size 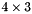$ 4 \times 3 $ (major dimensions):

sparse-matrix.png

Such matrix can be created with the following code:

QVSparseBlockMatrix sparseM(4,3,3,5);

Initially, the matrix is created empty. To initialize the blocks that contain elements different from zero, we can use the method setBlock:

sparseM.setBlock(0, 0, QVMatrix::random(3,5));
sparseM.setBlock(0, 2, QVMatrix::random(3,5));
sparseM.setBlock(1, 1, QVMatrix::random(3,5));
sparseM.setBlock(2, 0, QVMatrix::random(3,5));
sparseM.setBlock(2, 2, QVMatrix::random(3,5));
sparseM.setBlock(3, 0, QVMatrix::random(3,5));

The [] operator can substitute the setBlock method. The previous code is equivalent to the following code:

sparseM[0][0] = QVMatrix::random(3,5);
sparseM[0][2] = QVMatrix::random(3,5);
sparseM[1][1] = QVMatrix::random(3,5);
sparseM[2][0] = QVMatrix::random(3,5);
sparseM[2][2] = QVMatrix::random(3,5);
sparseM[3][0] = QVMatrix::random(3,5);

However, it is recomendable to use the method setBlock to initialize the contents of the blocks in the sparse matrices. The latter method performs several checks on the dimensions of the input matrices, and the ranges of the sparse matrix, to avoid invalid matrix assignments.

The previous code example initializes the non-zero blocks of the sparse matrix with matrices containing random values, but other matrices with compatible dimensions could of course be used as well.

We can convert the sparse matrix to a dense QVMatrix and print it on the console:

QVMatrix M = sparseM;
std::cout << "M = " << M << std::endl;

The console output of the previous code will be the following:

M = QVMatrix (12, 15)
[
    [ 0.3943 0.7682 0.5134 0.6069 0.4009 0.0000 0.0000 0.0000 0.0000 0.0000 0.8391 0.9727 0.8915 0.9493 0.3488 ]
    [ 0.7984 0.5539 0.9161 0.2428 0.1088 0.0000 0.0000 0.0000 0.0000 0.0000 0.2960 0.7713 0.3524 0.0860 0.0200 ]
    [ 0.1975 0.6288 0.7172 0.8041 0.2182 0.0000 0.0000 0.0000 0.0000 0.0000 0.5242 0.7699 0.9190 0.6632 0.0630 ]
    [ 0.0000 0.0000 0.0000 0.0000 0.0000 0.9706 0.7602 0.9318 0.3540 0.3303 0.0000 0.0000 0.0000 0.0000 0.0000 ]
    [ 0.0000 0.0000 0.0000 0.0000 0.0000 0.8509 0.6677 0.7209 0.1659 0.8933 0.0000 0.0000 0.0000 0.0000 0.0000 ]
    [ 0.0000 0.0000 0.0000 0.0000 0.0000 0.5397 0.0392 0.7385 0.8800 0.6866 0.0000 0.0000 0.0000 0.0000 0.0000 ]
    [ 0.5886 0.8147 0.9201 0.2810 0.2762 0.0000 0.0000 0.0000 0.0000 0.0000 0.1260 0.3831 0.2444 0.7450 0.2400 ]
    [ 0.8586 0.9109 0.8810 0.3074 0.4165 0.0000 0.0000 0.0000 0.0000 0.0000 0.7604 0.3686 0.7321 0.9501 0.7326 ]
    [ 0.9239 0.2158 0.4319 0.2261 0.9068 0.0000 0.0000 0.0000 0.0000 0.0000 0.9350 0.2322 0.7934 0.5215 0.9674 ]
    [ 0.7597 0.2046 0.1578 0.0540 0.1803 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 ]
    [ 0.1349 0.8196 0.2043 0.0723 0.3916 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 ]
    [ 0.0782 0.7555 0.1254 0.9230 0.8196 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 ]
]

One very interesting thing to do with sparse matrices is, of course, solving (sparse) linear systems of equations involving a sparse matrix of coefficients. You can do that using the SparseSolve function from the matrix algebra module of QVision. Here is an example, which solves the system 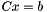$ C x = b $, with:

$ C = \left( \begin{array}{ccccc} 9 & 1.5 & 6.0 & 0.75 & 3.0 \\ 1.5 & 0.5 & 0.0 & 0.0 & 0.0 \\ 6.0 & 0.0 & 12.0 & 0.0 & 0.0 \\ 0.75 & 0.0 & 0.0 & 0.625 & 0.0 \\ 3.0 & 0.0 & 0.0 & 0.0 & 16.0 \\ \end{array} \right) $

and

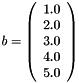
$ b = \left( \begin{array}{c} 1.0 \\ 2.0 \\ 3.0 \\ 4.0 \\ 5.0 \\ \end{array} \right) $

Observe that the C matrix is symmetric and positive definite, in this example.

Here is the corresponding code (in this simple example, each individual subblock matrix is simply of size 1x1):

#include <iostream>
#include <QVMatrix>
#include <QVVector>
#include <QVSparseBlockMatrix>

int main(int argc, char *argv[])
{
        QVSparseBlockMatrix C(5,5,1,1);

        C.setBlock(0,0,QVMatrix(1,1,9.0));
        C.setBlock(0,1,QVMatrix(1,1,1.5));
        C.setBlock(0,2,QVMatrix(1,1,6.0));
        C.setBlock(0,3,QVMatrix(1,1,0.75));
        C.setBlock(0,4,QVMatrix(1,1,3.0));
        C.setBlock(1,1,QVMatrix(1,1,0.5));
        C.setBlock(2,2,QVMatrix(1,1,12.0));
        C.setBlock(3,3,QVMatrix(1,1,0.625));
        C.setBlock(4,4,QVMatrix(1,1,16.0));

        QVVector x , b = QVVector() << 1.0 << 2.0 << 3.0 << 4.0 << 5.0 ;

        // First true stands for symmetric, second for positive definite matrix:
        sparseSolve(C, x, b, true , true, QVMKL_DSS);

        std::cout << "Vector b:" << b << "\n";
        std::cout << "Matrix C:" << C << "\n";
        std::cout << "Vector x:" << x << "\n";
}

The solution vector x for this example is:

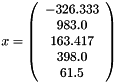
$ x = \left( \begin{array}{c} -326.333 \\ 983.0 \\ 163.417 \\ 398.0 \\ 61.5 \\ \end{array} \right) $

Note that in this case only the upper triangular part of the C matrix has to be initialized (because it is symmetric, as indicated by the 'true' second argument to the sparseSolve function). Also, the 'true' in the third argument indicates to the underlying solver that the C matrix is positive definite, a fact which can be used to accelerate computation.

Definition at line 172 of file qvsparseblockmatrix.h.

Constructor & Destructor Documentation

QVSparseBlockMatrix::QVSparseBlockMatrix (  )  [inline]

Default constructor for the QVSparseBlockMatrix class.

Definition at line 180 of file qvsparseblockmatrix.h.

QVSparseBlockMatrix::QVSparseBlockMatrix ( const int  majorRows,
const int  majorCols,
const int  minorRows,
const int  minorCols 
) [inline]

Create a sparse block matrix of a given size.

This constructor creates a sparse matrix of size $ majorRows minorRows \times majorCols minorCols $. Every element of the matrix will contain the $ 0 $ value.

Parameters:
majorRows Number of rows of block matrices.
majorCols Number of columns of block matrices.
minorRows Number of rows of the block matrices.
minorCols Number of columns of the block matrices.

Definition at line 201 of file qvsparseblockmatrix.h.

QVSparseBlockMatrix::QVSparseBlockMatrix ( const int  majorRows,
const int  majorCols,
const QVMatrix &  other 
) [inline]

Create a sparse block matrix from a dense matrix.

This constructor creates a sparse matrix of size 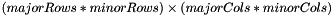$ (majorRows * minorRows) \times (majorCols * minorCols) $. The elements of the sparse matrix will be initialized with the contents of the matrix passed by parameter (adequately partitioned in blocks of the given size, and with any zero submatrix of the input matrix conveniently "supressed" from the internal representation).

The following two identities must hold when calling this method (otherwise, it will fail):

  • (other.getRows() / majorRows) * majorRows == other.getRows()
  • (other.getCols() / majorCols) * majorCols == other.getCols()
Parameters:
majorRows Number of rows of block matrices.
majorCols Number of columns of block matrices.
minorRows Number of rows of the block matrices.
minorCols Number of columns of the block matrices.
other Dense matrix containing the values to initialize the sparse matrix.

Definition at line 221 of file qvsparseblockmatrix.h.

Member Function Documentation

int QVSparseBlockMatrix::getMajorRows (  )  const [inline]

Get majorRows from a sparse block matrix.

Definition at line 243 of file qvsparseblockmatrix.h.

Referenced by incrementalGEA(), and sparseSolve().

int QVSparseBlockMatrix::getMajorCols (  )  const [inline]

Get majorCols from a sparse block matrix.

Definition at line 246 of file qvsparseblockmatrix.h.

Referenced by incrementalGEA(), solveHomogeneous(), and sparseSolve().

int QVSparseBlockMatrix::getMinorRows (  )  const [inline]

Get minorRows from a sparse block matrix.

Definition at line 249 of file qvsparseblockmatrix.h.

Referenced by incrementalGEA(), and sparseSolve().

int QVSparseBlockMatrix::getMinorCols (  )  const [inline]

Get minorCols from a sparse block matrix.

Definition at line 252 of file qvsparseblockmatrix.h.

Referenced by incrementalGEA(), solveHomogeneous(), and sparseSolve().

QVSparseBlockMatrix::operator QVMatrix (  )  const [inline]

Convert a sparse block matrix into an ordinary matrix.

Definition at line 255 of file qvsparseblockmatrix.h.

void QVSparseBlockMatrix::setBlock ( const int  majorRow,
const int  majorCol,
const QVMatrix &  M 
) [inline]

Set a data block.

You can set a block submatrix in the sparse matrix with this method. The following two lines of code are equivalent: 

 QVSparseBlockMatrix M(10,20, 3, 3);
 [...]
 M[7][10] = QVMatrix::identity(3);
 M.setBlock(7,10, QVMatrix::identity(3));

Setting the block of a sparse matrix using this method is safer than with the [] operators. This method will check the index ranges, and the correct size of the input matrix for the block.

Parameters:
majorRow Row index of the block, inside the sparse matrix.
majorCol Column index of the block, inside the sparse matrix.
M Matrix with the contents of the block.

Definition at line 288 of file qvsparseblockmatrix.h.

Referenced by incrementalGEA(), and randomSquare().

QVMatrix& QVSparseBlockMatrix::getBlock ( const int  majorRow,
const int  majorCol 
) [inline]

Gets a data block.

Definition at line 314 of file qvsparseblockmatrix.h.

bool QVSparseBlockMatrix::isNullBlock ( const int  majorRow,
const int  majorCol 
) const [inline]

Evaluate if a block contains zero values.

This function can be used to evaluate if a block is undefined in the block-sparse matrix.

Returns:
true if the block matrix is Null. This implies that every element of the block matrix is zero. A false value on the output does not imply that the elements of the block matrix differ from zero in any case.

Definition at line 339 of file qvsparseblockmatrix.h.

QList<int> QVSparseBlockMatrix::getBlockRowIndexes ( const int  majorRow  )  const [inline]

List of non-zero blocks in a block-row.

This function returns a list of the blocks in a block-row of the sparse matrix which are non-zero.

Parameters:
majorRow block-row index.

Definition at line 393 of file qvsparseblockmatrix.h.

QVSparseBlockMatrix QVSparseBlockMatrix::operator* ( const QVSparseBlockMatrix &  other  )  const [inline]

Product operator for sparse block matrices.

The sparse block matrices must have compatible block sizes, and major sizes.

Parameters:
other factor for the product operator.

Definition at line 403 of file qvsparseblockmatrix.h.

QVVector QVSparseBlockMatrix::operator* ( const QVVector &  vector  )  const [inline]

Sparse block matrix-vector product.

Parameters:
vector vector to multiply by.

Definition at line 408 of file qvsparseblockmatrix.h.

QVSparseBlockMatrix QVSparseBlockMatrix::dotProduct ( const QVSparseBlockMatrix &  other,
const bool  transposeFirstOperand = false,
const bool  transposeSecondOperand = false 
) const

Dot product for sparse block matrices.

The sparse block matrices must have compatible block sizes, and major sizes.

Parameters:
other factor for the product operator.

Todo:
mejorar operador de incremento para matrices

Definition at line 43 of file qvsparseblockmatrix.cpp.

Referenced by incrementalGEA(), operator*(), and randomSquare().

QVVector QVSparseBlockMatrix::dotProduct ( const QVVector &  vector,
const bool  transposeMatrix = false 
) const

Dot product for sparse block matrices with vectors.

The sparse block matrix must have compatible block sizes, and major sizes, with the vecto size

Parameters:
vector factor for the product operator.

Todo:
mejorar operador de incremento para vectores

Definition at line 100 of file qvsparseblockmatrix.cpp.

QVSparseBlockMatrix & QVSparseBlockMatrix::operator= ( const QVSparseBlockMatrix &  other  ) 

Copy operator.

Definition at line 144 of file qvsparseblockmatrix.cpp.

void QVSparseBlockMatrix::clear (  )  [inline]

Set matrix to zero.

Definition at line 430 of file qvsparseblockmatrix.h.

QVSparseBlockMatrix QVSparseBlockMatrix::randomSquare ( const int  NB,
const int  N,
const double  NZProb,
const bool  symmetric = true,
const bool  positive = true 
) [static]

Generates a random square sparse block matrix The sparse block matrix must have compatible block sizes, and major sizes, with the vecto size.

Parameters:
NB number of row (=column) blocks
NB number of rows (=columns) by block
NZProb probability of a block of being of different from zero (out of diagonal) in generated matrix
symmetric if the matrix to be generated should be symmetric
positive if the matrix to be generated should be positive definite
Returns:
the generated sparse square block matrix

Definition at line 165 of file qvsparseblockmatrix.cpp.

The documentation for this class was generated from the following files:


QVision framework. PARP research group. Copyright © 2007, 2008, 2009, 2010, 2011.